Simpira is a family of cryptographic permutations (paper, slides, video, source code). It is designed to be fast on modern 64-bit processors, yet provide a comfortable security margin against all currently-known attacks.
More specifically,
- On Intel Skylake, Simpira’s throughput is below 1 cycle/byte for inputs of up to 64 bytes, and 1.44 cycles/byte for an input of 512 bytes.
- Simpira is designed to be secure against structural distinguishers with complexity up to 2128.
Simpira is the result of a collaboration between Shay Gueron and Nicky Mouha.
Contents
Updates
December 18, 2016: In ePrint 2016/1161, Zong et al. construct impossible differentials for Simpira for b=4 (512-bit inputs). With these impossible differentials, they construct key recovery attacks on 7 out of 15 rounds of Simpira, assuming that the attacker cannot perform more than 2128 permutation evaluations. Without this restriction, they show how to attack 8 out of 15 rounds.
December 5, 2016: Simpira was presented at the ASIACRYPT 2016 conference in Hanoi, Vietnam.
April 21, 2016: Forler et al. use Simpira to achieve an efficient beyond-birthday-bound-secure construction for deterministic authenticated encryption.
March 6, 2016: The 512-bit permutation of the initial Simpira was vulnerable to two attacks: one by Dobraunig et al. and another by Rønjom. To prevent the attacks, Simpira v2 replaces the problematic Type-1.x GFS of Yanagihara and Iwata by a new construction. The round constants were also strengthened, although no attack is known on Simpira v2 with the old round constants.
Applications
A cryptographic permutation is a building block that can be used for encryption, authentication and hashing.
Simpira is well-suited for applications where the 128-bit block size of AES is not sufficient, but a wider range of block sizes is required. We refer to the paper for a detailed overview of applications, such as wide-block encryption, short-input hashing or robust authenticated encryption.
Using the 256-bit permutation inside the Even-Mansour construction results in an efficient 256-bit block cipher with 128-bit multi-key security. It is also an efficient solution to achieve security beyond 264 data blocks, which is the birthday bound beyond which typical AES-based modes of operation become insecure. An interesting implementation feature is that this block cipher avoids the overhead of a key schedule.
Design
Simpira supports inputs of 128 × b bits. We will provide an overview of the design that omits several details. A full specification is given in the paper, and a reference implementation is available as well.
First, we describe Simpira for small values of b. Simpira follows a recursive construction for large b, which we will describe afterwards. Depending on the value of b, one of the following round functions is iterated:
On Intel and AMD processors, the F-function can be implemented by two AESENC instructions. This AESENC instruction includes an XOR with a round key, which is used to introduce a round constant in the first AES round, and to do a “free XOR” in the second AES round. Simpira can therefore described in terms of only AES rounds. We hope that this will maximize the contribution of every instruction to the security of the overall design.
The number of rounds is determined as follows. We calculate the number of rounds to achieve at least 25 active S-boxes (linearly or differentially), as well as the number of rounds to reach full diffusion (for the forward and the inverse permutation). The largest of these two numbers is multiplied by three to obtain the total number of rounds. Consequently, the number of rounds for is 12 for b=1, 15 for b=2, b=4 and b=6, 21 for b=3, and 18 for b=8.
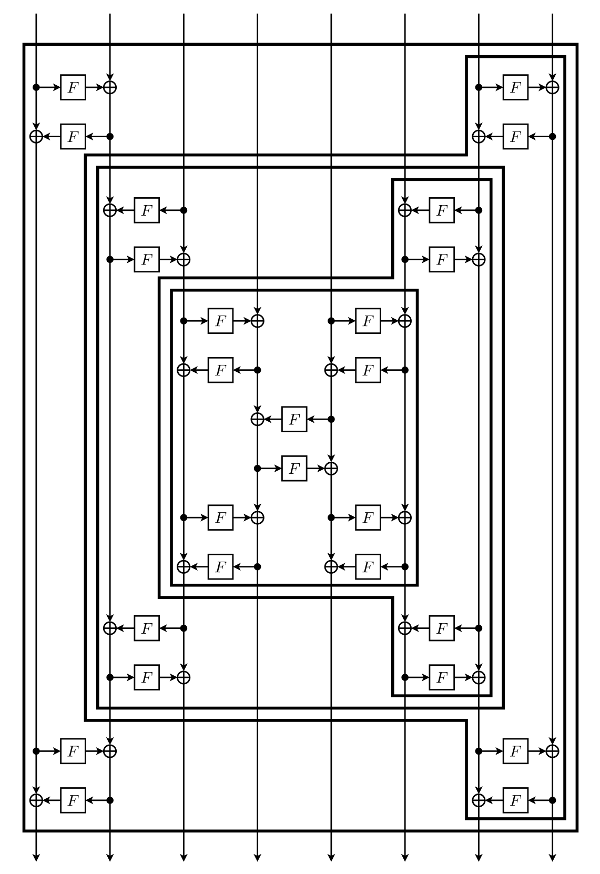
For other values of b, Simpira is based on the recursive construction, as shown below. It achieves full diffusion and ensures at least 25 active S-boxes. This construction is iterated three times. By convention, the leftmost F-function is from left to right; when this is not the case in the diagram, the direction of every F -function should be inverted.
Benchmarks
We benchmarked Simpira on the latest Intel processor, Architecture Codename Skylake. For every b, we measured the throughput given four independent inputs. The data is either stored sequentially at different pointers, or in interleaved buffers. We give the number of cycles to process the four inputs, as well as the overhead compared to performing only AESENC instructions.
| non-interleaved | interleaved | |||||
| b | bits | # AESENC | cycles (4×) | overhead | cycles (4×) | overhead |
| 1 | 128 | 12 | 50 | 3% | 50 | 3% |
| 2 | 256 | 30 | 122 | 1% | 122 | 1% |
| 3 | 384 | 42 | 171 | 2% | 171 | 2% |
| 4 | 512 | 60 | 241 | 1% | 241 | 1% |
| 6 | 768 | 90 | 362 | 1% | 362 | 1% |
| 8 | 1024 | 144 | 594 | 3% | 594 | 3% |
| 16 | 2048 | 348 | 1586 | 14% | 1400 | 1% |
| 32 | 4096 | 732 | 3295 | 13% | 2946 | 1% |
| 64 | 8192 | 1500 | 6791 | 13% | 6040 | 1% |
| 128 | 16384 | 3036 | 13942 | 15% | 12220 | 1% |
| 256 | 32768 | 6108 | 31444 | 29% | 24799 | 2% |